| SuDiBe Tandemseiten |
|
Die Synchronkette des Tandems heißt so, weil sie die Kurbelsätze von Captain und Stoker in einer festen 1:1-Übersetzung miteinander verbindet. Aber müssen beide Fahrer auch ihre Kurbeln immer am selben Ort haben, also in Phase fahren? Sie müssen natürlich nicht, obwohl die meisten Tandems so eingestellt sind, dass sie diesem Idealbild möglichst nahe kommen, also einer Phasenverschiebung 0 °. Bei Tandems mit unabhängigem Freilauf kann die Phasenverschiebung während der Fahrt verändert werden, allerdings ist diese Lösung aus mehreren Gründen ungebräuchlich.
Kleine Abweichungen vom exakten Gleichtritt sind ohnehin kaum vermeidbar, weil die Kettenblätter des Synchronantriebs selten völlig gleich sind bzw. in der gleichen Position an den Kurbelsternen befestigt sind. Bei einer Größe der Synchronblätter von 36 Zähnen ergibt schon ein einziger Zahn Abweichung eine Phasenverschiebung von 10 °. Bei zufällig montierten Synchronblättern liegt man also zwischen 0 und maximal 5 Grad (einen halben Zahn) daneben. Nach unfreiwilligem Kettenabwurf und hektischem Wiederauflegen im Gelände kann man schon mal ein paar Zähne daneben liegen. Meist fällt das gar nicht gleich auf.

Synchronantrieb ohne Phasenverschiebung (0 °). (weitere Bilder folgen)
Wie groß kann die Phasenverschiebung eigentlich sein? Eine Umdrehung der Kurbeln sind 360 °. Infolgedessen kann auch die Phasenverschiebung zwischen 0 ° und 360 ° liegen. 359 ° sind aber fast wieder 0 °. Deshalb teilen wir den Kreis in zwei Halbkreise auf: Captain führt 0° bis 180 ° oder Stoker führt 0° bis 180 °. Bei einer Phasenverschiebung von mehr als 90 ° treten die beiden Fahrer wieder zeitnäher als bei 90 °, bei 180 ° treten beide zwar gleichzeitig, aber jeweils auf der gegenüberliegenden Seite. Diese Fälle lassen wir bei der Betrachtung gleich weg. Es bleiben daher 3 Fälle übrige: Gleichtritt (0 °), Stoker führt (0 ° bis 90 °) oder Captain führt (0 ° bis 90 °).
Was spricht nun für Gleichtritt und was für eine gewisse Phasenverschiebung? Die am häufigsten genannten Argumente sind in etwa folgende:
Für Gleichtritt
Für Phasenverschiebung
Bei beiden Varianten gibt es also Vor- und Nachteile. Die Argumente für eine Phasenverschiebung sind also hauptsächlich technischer Natur, während für den Gleichtritt hauptsächlich ein besserer Fahrstil spricht. Da das eine offenbar nicht gleichzeitig mit dem anderen zu verwirklichen ist, soll im Folgenden betrachtet werden, ob es sich lohnen könnte, Kompromisse einzugehen, also z.B. mit einer Phasenverschiebung von 30 ° zu fahren.
Es gibt ein paar frei zugängliche Quellen, die Messungen von Drehmomentverläufen von Radfahrern angeben. Die folgende Abbildung zeigt an Bahnrennfahrern gemessene Drehmomentverläufe für eine einzelne Kurbel, also die rechte oder die linke, die als identisch angenommen werden [1]. Auf der senkrechten Achse ist die Tangentialkraft am Pedal aufgetragen, die direkt proportional zum Drehmoment ist.
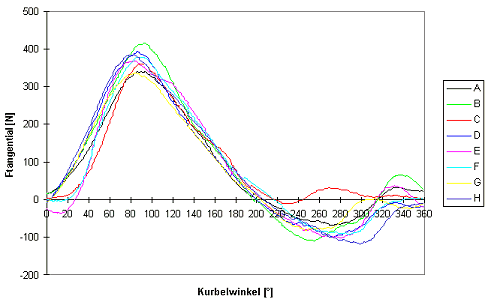
Gemessene Momentverläufe aus [1], jeweils für eine Kurbel.
Das Drehmoment ist also am größten, wenn sich der Fuß nach unten bewegt - klar. Aber auch an den beiden "Totpunkten" der Bewegung wird das Moment meistens nicht ganz Null. Besonders bei 180 °, also am unteren "Totpunkt", wurde bei allen Probanden ein deutliches Moment gemessen. Interessant ist, dass selbst gute Rennfahrer offenbar in der Aufwärtsbewegung nicht wirklich am Pedal ziehen, aber immerhin das Eigengewicht des Beins ausgleichen. Dieses Verhalten mag insgesamt qualitativ dem Muskeleinsatz beim Laufen entsprechen. In der nächsten Abbildung ist ein Versuch dargestellt, eine reale Drehmomentkurve mit einer möglichst einfachen Formel anzunähern. Die grün dargestellt Sinus-Quadrat-Funktion wurde mit der braunen Kurve multipliziert. Das Ergebnis ist die blaue Kurve, die den Drehmomentverlauf annähern soll. Das Maximum dieser Kurve ist auf den Wert 1 normiert.
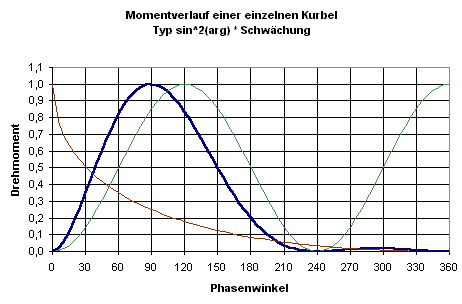
Mit Näherungsformel berechneter Momentverlauf für eine Kurbel.
Für die Berechnung des Drehmomentverlaufs eines Fahres bzw. des Verlaufs am Solorad müssen 2 derartige Kurven um 180 phasenverschoben addiert werden. Dies ist in der folgenden Abbildung dargestellt.
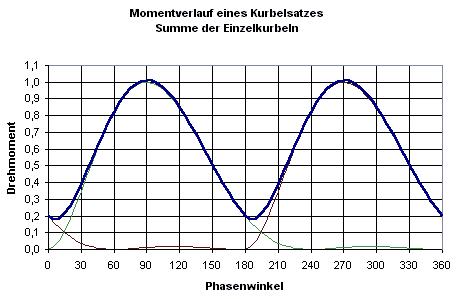
Berechnung des Momentverlaufs eines Kurbelsatzes durch Addition zweier Einzelkurbeln mit 180 Grad Phasenversatz.
Interessant ist dabei, dass das Drehmoment nie wirklich bis auf Null abfällt. Deshalb wird hier "Totpunkt" immer in Anführungszeichen geschrieben - es gibt nämlich keinen. Ein minimales Drehmoment liegt immer an. Für ein Tandem mit 2 Fahrern müssen nun 2 der eben berechneten Kurven addiert werden. Dies kann nach unserer oben gemachten Fallunterscheidung mit Phasenversätzen zwischen -90° und 90 ° geschehen. Das Beispiel im folgenden Bild verlegt die Bewegung eines Fahrers um 30 ° nach vorne. Dies definieren wir als eine positive Verschiebung, also +30 °.
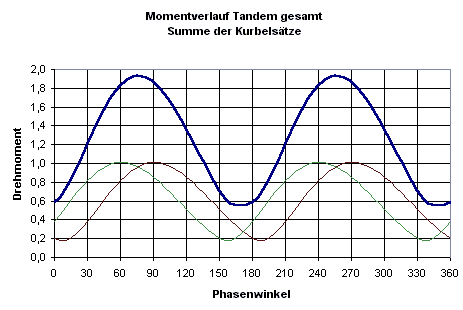
Berechnung des Momentverlaufs am Tandem durch Addition zweier Kurbelsätze, hier mit 30 Grad Phasenversatz.
Nach dieser Vorbereitung kann die Phasenverscheibung systematisch variiert werden. Dies geschieht im folgenden Bild, in dem Phasenverschiebungen von 0°, 30 °, 60 ° und 90 ° eingetragen sind. Zum Vergleich ist die Drehmomentkurve des in der Bewegung nachfolgenden Fahrers dargestellt.
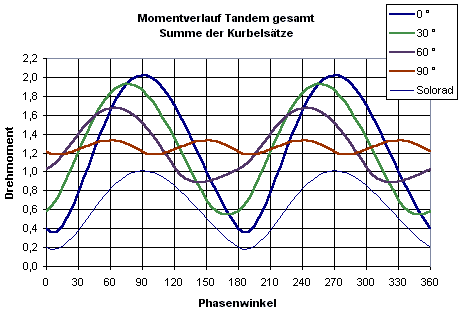
Vergleich der Momentverläufe am Tandem bei unterschiedlichem Phasenversatz.
Bei Gleichtritt ist das maximale Drehmoment genau doppelt so hoch wie bei einem einzelnen Fahrer - logisch (Voraussetzung ist übrigens immer, dass beide Fahrer genau die gleich Tretbewegung mit derselben Kraft durchführen). Eine Phasenverschiebung von 30 ° hat einen recht schwachen Effekt. Bei 60 ° wird das maximale Drehmoment um gut 15 % verringert. Erst danach wird ein deutlich spürbarer Effekt erzielt. Bei der maximalen Phasenverschiebung von 90 °, wenn also die Pedalen von Captain und Stoker senkrecht zueinander stehen, reduziert sich die Maximalbelastung um ca. 35 % und ist damit ca. 35 % größer als am Solorad. Mehr ist nicht drin, jedenfalls nicht bei der verwendeten Drehmomentkurve für die Einzelkurbel.
Es ist also nicht so, dass sich durch 90 ° Phasenversatz das maximale Drehmoment am Tandem halbieren lässt. Dies wäre dann der Fall, wenn die Drehmomentkurve für jede Kurbel eine reine Sinus-Quadrat-Funktion wäre, die bei 0 ° und bei 180 ° auf Null abfällt, also echte Totpunkte hätte. Möglicherweise kommen Drehmomentkurven von ungeübten Radfahrern einer solchen Funktion näher als diejenigen von gut trainierten Rennfahrern.
In Anbetracht der oben gezeigten Vor- und Nachteile sowie der quantitativ abgeschätzen Effekte mag jedes Team für sich entscheiden, ob Phasenversatz etwas bringt oder nicht. Im Zweifelsfall geht natürlich auch in dieser Angelegenheit Probieren über Studieren.
Wie schon erwähnt, kann bei mehr-als-zwei-sitzigen Tandems nur eine geschickte Phasenverschiebung aller Kurbelsätze die sofortige Zerstörung der Hinterradnabe verhindern. Die allgemeiner Formel für die Phasenverschiebung ist in solchen Fällen 180°/n, wobei n die Zahl der Fahrer ist. Bei einem Quint sind das dann 180°/5=36°. Im folgenden Bild wurde dieses Prinzip angewendet.


Quint mit versetzten Kurbelsätzen. Fotos: Wolfgang Haas
Dank an verschiedene Mitglieder von der Mailingliste auf tandem-fahren.de für diverse Anregungen.